Analoge Grundlagen - Teil 4: Optimierung von Delta-Sigma-ADCs für geringes Rauschen
Zur Verfügung gestellt von Nordamerikanische Fachredakteure von DigiKey
2020-08-05
Anmerkung der Redaktion: Analog/Digital-Wandler (ADCs) verbinden die analoge mit der digitalen Welt und sind somit eine grundlegende Komponente jedes elektronischen Systems, das eine Verbindung zur realen Welt herstellt. Sie sind auch ein entscheidender Bestimmungsfaktor für die Leistung eines Systems. In dieser Reihe werden die Grundlagen der ADCs, ihre verschiedenen Arten und ihre Anwendung untersucht. Teil 1 dieser Serie über analoge Grundlagen diskutierte SAR-ADCs. Teil 2 befasst sich mit Delta-Sigma-Wandlern. Teil 3 befasst sich mit den Pipeline-ADCs. Hier wird in Teil 4 gezeigt, wie Delta-Sigma-ADCs extrem rauscharme Ergebnisse erzielen können. Teil 5 befasst sich mit schwierigen Eingangs-Treiberfragen für SAR-ADCs.
Die Delta-Sigma(ΔƩ)-Topologie wird auch heute noch häufig in Analog/Digital-Wandlern (ADCs) verwendet und bietet Lösungen mit hoher Auflösung, hoher Integration und geringem Stromverbrauch für Prozesssteuerung, Präzisionstemperaturmessung und Waagenanwendungen.
Das Rätselhafte an diesem Wandlertyp ist, dass er mit einer 1-Bit-Wandlung mit einem theoretischen Signal-Rausch-Verhältnis (SNR) von 7,78 Dezibel (dB) beginnt, was einem Rauschen von 2 Volt (Veff) in einem 5-Volt-System entspricht. Von dort aus kann der ADC zu einem echten 24-Bit-Delta-Sigma-Wandler aufblühen, der ein theoretisches SNR von 146 dB liefert, was einem Rauschen von 244 Nanovolt (nV(eff)) in einem 5-Volt-System entspricht.
Dieser Auflösungssprung von 1 Bit auf 24 Bit beruht auf Oversampling-Algorithmen, rauschformenden Modulatoren und digitalen Filtern, um das Quantisierungsrauschen zu verringern und das SNR zu erhöhen. Es gibt eine Möglichkeit, die Komplexität des ΔƩ Wandlers und das damit verbundene Rauschen zu vermeiden, indem stattdessen eine Verstärkereingangsstufe verwendet wird, die in einen 12- oder 16-Bit-ADC mit sukzessivem Näherungsregister (SAR) einspeist. Dieser Designweg wird funktionieren, aber er erfordert mehr integrierte Schaltungen auf der Leiterplatte und eine größere Stückliste.
Es gibt einen besseren Weg, das Problem des Rauschens anzugehen: verwenden Sie einfach einen ultra-rauscharmen ΔƩ-ADC.
Dieser Artikel beschreibt kurz die rauscharme Zielanwendung und wie der ΔƩ-ADC intern so gestaltet ist, dass er diese Anforderung erfüllt. Anschließend werden zwei ΔƩ-ADCs von Texas Instruments vorgestellt - einer mit Schwerpunkt auf 24-Bit-Präzision, der andere mit Schwerpunkt auf 32-Bit-Präzision - und es wird gezeigt, wie die Vorteile der robusten digitalen Filterung in beiden genutzt werden können.
Wo der ΔƩ-ADC passt
Aus analoger Sicht benötigen Ingenieure verschiedene Genauigkeitsgrade bei der Messung der Ausgabe von Temperatur-, Druck-, Wägezellen- und optischen Sensoren. Grundsätzlich verbessern Verstärker die Fähigkeit von Konstrukteuren, diese kleinen und in den meisten Fällen in der Nähe von Gleichstrom auftretenden analogen Erscheinungen zu quantifizieren. Die fortschreitende Digitalisierung hat eine Veränderung der Perspektive und der Fähigkeiten bewirkt und gleichzeitig die Fähigkeit verbessert, die Sensorsignale zu speichern und zu modifizieren.
Ein typischer Sensorsignalpfad zur digitalen Erfassung beginnt mit dem Sensor, durchläuft die Verstärkungs-, Multiplex- und Filterstufen und gelangt dann zum ADC (Abbildung 1a).
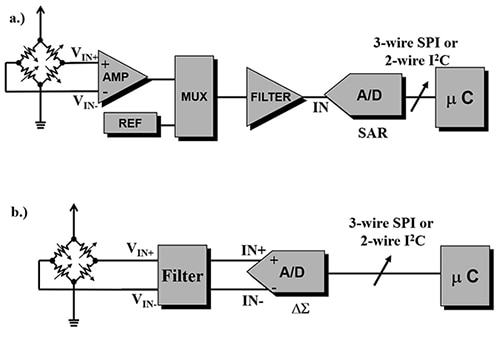 Abbildung 1: Zwei Techniken zur Digitalisierung eines Sensorsignals verwenden SAR-ADCs (a) oder ΔƩ-ADCs (b). Für hochauflösende Schaltungen erfordert der SAR-ADC eine Verstärkung und einen aktiven Filter fünfter Ordnung, während der ΔƩ-ADC einen analogen passiven Filter erster Ordnung als Front-End benötigt. (Bildquelle: A Baker’s Dozen: Real Analog Solutions for Digital Designers, B. Baker, ISBN 0-7506-7819-4)
Abbildung 1: Zwei Techniken zur Digitalisierung eines Sensorsignals verwenden SAR-ADCs (a) oder ΔƩ-ADCs (b). Für hochauflösende Schaltungen erfordert der SAR-ADC eine Verstärkung und einen aktiven Filter fünfter Ordnung, während der ΔƩ-ADC einen analogen passiven Filter erster Ordnung als Front-End benötigt. (Bildquelle: A Baker’s Dozen: Real Analog Solutions for Digital Designers, B. Baker, ISBN 0-7506-7819-4)
Bei dem Wandler in Abbildung 1a handelt es sich um einen SAR-ADC, der 12-Bit-zu-18-Bit-Wandlungen durchführen kann und mit einer Wandlungsrate von bis zu 10 Megasamples pro Sekunde (MS/s) betrieben werden kann. Der 16-Bit-Konverter bietet 216 oder 65.536 Segmente. In einem 5-Volt-System ist das niederwertigste Bit (LSB) 5 Volt/216298 oder 76,3 Mikrovolt (mV), mit einem theoretischen SNR von 98 dB. Es ist möglich, eine höhere Granularität zu erreichen, indem man die analoge Verstärkung vor dem SAR-Wandler ausübt.
Die ΔƩ-Signalkette (Abbildung 1b) verbessert die Auflösung der Signalkette mit einem einzigen Konverter, was auch die Stückliste senkt. Der ΔƩ-ADC kann 16-Bit-zu-32-Bit-Konvertierungen anbieten. In dieser Signalkette bietet der 24-Bit-ΔƩ-ADC 224 oder 16.777.216 Segmente. In einem 5-Volt-System beträgt das LSB daher 5 Volt/224, oder 298 nV, mit einem theoretischen SNR von 146 dB. Dieses Auflösungsniveau bringt die Konvertergranularität näher an die Fähigkeiten des Sensors.
Der 24-Bit-ΔƩ-ADC ist langsamer aufgrund der internen digitalen Filter, die Zeit benötigen, um Filterberechnungen zu implementieren. Typische Ausgangsdatenraten für diesen Konverter reichen von einigen Hertz bis zu 1 MS/s. Beachten Sie, dass der Analogfilter jetzt ein kostengünstiger Widerstands-Kondensator-Filter (RC-Filter) erster Ordnung ist, anstatt des komplexen, aus drei Operationsverstärkern bestehenden Analogfilters fünfter Ordnung.
Die Unterschiede zwischen dem Rauschen dieser beiden Ansätze sind deutlich: Der ΔƩ-ADC übertrifft mit seinem geringen Rauschen den SAR-ADC (Tabelle 1).
*Anmerkung: SNR = 6,02 N + 1,76, wobei N die Anzahl der Bits ist.
|
Tabelle 1: ADC-Segmente, LSB und theoretischer SNR mit einer Vollbereichseingangsspannung von 5 Volt für einen 16-Bit-SAR-ADC und einen 24-Bit-ΔƩ-ADC. (Datenquelle: DigiKey)
Der ΔƩ-ADC bietet eine ausgezeichnete Lösung für Sensorlösungen, wie z.B. Temperatur, Druck und Wägezellen, bei denen die Spezifikation der Geschwindigkeit nicht kritisch ist; die Genauigkeit ist jedoch von größter Bedeutung. Dieser ADC kann auf diese kleinen Spannungswerte herunterkonvertieren, indem er digitale anstelle von analogen Rauschunterdrückungstechniken verwendet.
Innerhalb des ΔƩ-ADC
Das Innere des ΔƩ-ADC ist zu 80% digital. Normalerweise empfängt der Konverter das Eingangssignal und wandelt dieses analoge Signal sofort in ein digitales um. Der Wandler kombiniert dann dieses digitale Signal mit nachfolgenden Modulator-Umwandlungen in eine digitale Filterstufe, in der das akkumulierte 1-Bit-Signal in mehrere Bits umgewandelt wird. Der Wandler sendet dann seriell die endgültige Multi-Bit-Wandlung über die digitale Ausgangsstufe an den wartenden Mikrocontroller.
Das Analogsignal durchläuft zunächst einen externen Anti-Aliasing-Filter (AAF) erster Ordnung. Dann nimmt der NS-Modulator (Noise-Shaping, Rauschsignalformung) das analoge Signal und erzeugt einen 1-Bit-Strom mit der Taktrate des Wandlers in den digitalen Filter (Abbildung 2).
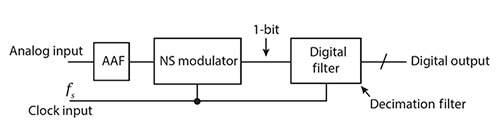 Abbildung 2: Der typische ΔƩ leitet das analoge Signal durch eine AAF erster Ordnung, erzeugt einen 1-Bit-Stream mit dem NS-Modulator und erzeugt dann ein Multi-Bit-Ergebnis am digitalen Ausgang zu einem Mikrocontroller. (Bildquelle: CMOS: Mixed-Signal Circuit Design, 2nd Edition, J. Baker, ISBN 978-0-470-29026-2)
Abbildung 2: Der typische ΔƩ leitet das analoge Signal durch eine AAF erster Ordnung, erzeugt einen 1-Bit-Stream mit dem NS-Modulator und erzeugt dann ein Multi-Bit-Ergebnis am digitalen Ausgang zu einem Mikrocontroller. (Bildquelle: CMOS: Mixed-Signal Circuit Design, 2nd Edition, J. Baker, ISBN 978-0-470-29026-2)
Der digitale Filter taktet mehrere Codes aus dem 1-Bit-Strom ein und erzeugt ein vollständiges Multi-Bit-Ergebnis im digitalen Filter. Diese Multi-Bit-Ergebnisse werden seriell über den digitalen Ausgang übertragen.
Der ΔƩ-Modulator
Die Anzahl der Integrator-/Rückkopplungsschleifen bestimmt die Ordnung des ΔƩ-Modulators. Der ΔƩ-ADC-Modulator erster Ordnung verfügt über einen einzigen Integrator und eine einzige Rückkopplungsschleife (Abbildung 3).
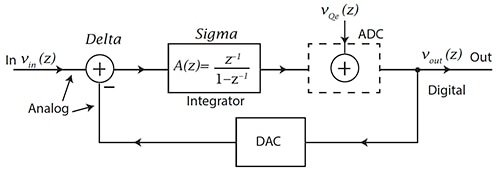 Abbildung 3: Modulator erster Ordnung mit einem analogen Integrator und 1-Bit-ADC und einem DAC in der Rückkopplungsschleife. VQe(z) ist das Quantisierungs-ADC-Rauschen. (Bildquelle: CMOS: Mixed-Signal Circuit Design, 2nd Edition, J. Baker, ISBN 978-0-470-29026-2)
Abbildung 3: Modulator erster Ordnung mit einem analogen Integrator und 1-Bit-ADC und einem DAC in der Rückkopplungsschleife. VQe(z) ist das Quantisierungs-ADC-Rauschen. (Bildquelle: CMOS: Mixed-Signal Circuit Design, 2nd Edition, J. Baker, ISBN 978-0-470-29026-2)
In Abbildung 3 tritt das Analogsignal (VIN(z)) in den Delta-Teil (Δ) des Modulators ein. Das Analogsignal durchläuft dann eine Integratorstufe oder Sigma-Stufe (Ʃ) zu einem 1-Bit-ADC (mit einer Abtastrate von fS, gemäß Abbildung 2), der ein Komparator sein kann. Dieses nun getaktete digitalisierte Signal wird zum 1-Bit-Digital/Analog-Wandler (DAC) zurückgeführt und geht auch zum VOUT(z) in der Stufe Δ über. Der 1-Bit-DAC stellt eine analoge Spannung dar, die vom analogen Eingangssignal subtrahiert wird, VIN(z). Die Übertragungsfunktion für diesen Modulator erster Ordnung ist:
![]() Gleichung 1
Gleichung 1
Aufgrund des Integrators und der Rückkopplungsschleife implementiert der Modulator einen Rauschformungsalgorithmus auf dem digitalen Ausgangsdatenstrom des Modulators (Abbildung 4).
 Abbildung 4: Die Rauschformungsfunktion am Ausgang des ΔƩ-Modulators, wobei die Rauschübertragungsfunktion (NTF) gleich 1-z-1 ist, wobei die 0,5-normalisierte Frequenz gleich FS/2 ist. (Bildquelle: Understanding Delta-Sigma Data Converters, Schreier, Temes, ISBN 0-471-46585-2)
Abbildung 4: Die Rauschformungsfunktion am Ausgang des ΔƩ-Modulators, wobei die Rauschübertragungsfunktion (NTF) gleich 1-z-1 ist, wobei die 0,5-normalisierte Frequenz gleich FS/2 ist. (Bildquelle: Understanding Delta-Sigma Data Converters, Schreier, Temes, ISBN 0-471-46585-2)
In Abbildung 4 ist die Rauschformungs-Charakteristik der erste Schritt zur Reduzierung des Umwandlungs-1-Bit-Quantisierungsrauschens. Nachdem das Rauschen erfolgreich in die höheren Frequenzen verschoben wurde, vervollständigt ein digitaler Tiefpassfilter den Prozess der Rauschunterdrückung.
Modulatoren höherer Ordnung enthalten zusätzliche Integratoren und Rückkopplungsschleifen. Zum Beispiel hat ein Modulator dritter Ordnung drei Integratoren und drei Rückkopplungsschleifen. Die Rauschformungsfunktion ändert sich mit der Modulatorordnung, indem das Rauschen in der Nähe von Gleichstrom reduziert und das geformte Rauschen erhöht wird.
Modulatoren höherer Ordnung bieten eine verbesserte Leistung auf Kosten von mehr Silizium-Hardware, geringerer Stabilität und Signalreichweite.
Die digitalen ΔƩ-Filter
Der ΔƩ-ADC arbeitet mit Oversampling (OS). Oversampling ist das Verhältnis der Abtastrate des Modulators (FS) zur ADC-Ausgangsdatenrate (FD) gemäß Gleichung 2:
![]() Gleichung 2
Gleichung 2
Oversampling verbessert ΔƩ-ADC-Rauschen durch digitale Bandbreitenbegrenzung der rauschförmigen Daten mit einem oder mehreren digitalen Tiefpassfiltern.
Die beiden am häufigsten verwendeten digitalen Filter im ΔƩ-ADC sind sin(pf)/pf (sinc) und linear-phasige Filter mit endlichem Impuls-Ansprechverhalten (FIR). Die Digitalfilter-Implementierung des ADS1235 von Texas Instruments, ein 24-Bit-ΔƩ-ADC, und der 32-Bit-ΔƩ-ADCs ADS1262 und ADS1263 (der ADS1263 integriert einen 24-Bit-ΔƩ-Hilfs-ADC für Hintergrundmessungen), bietet die Wahl zwischen der ausschließlichen Verwendung der Sinc-Filter oder einer Kombination von Sinc gefolgt von den FIR-Filtern (Abbildung 5).
 Abbildung 5: Der 24-Bit-ΔƩ-ADC ADS1235 bietet die ausschließliche Verwendung der Sinc-Filter oder eine Kombination von Sinc gefolgt von den FIR-Filtern an. (Bildquelle: Texas Instruments)
Abbildung 5: Der 24-Bit-ΔƩ-ADC ADS1235 bietet die ausschließliche Verwendung der Sinc-Filter oder eine Kombination von Sinc gefolgt von den FIR-Filtern an. (Bildquelle: Texas Instruments)
In Abbildung 5 ist der Sinc-Filter (mit „Sinc“ bezeichnet) ein digitaler Tiefpassfilter. Die Ausgabe (w(n)) eines Sinusfilters wird mit Gleichung 3 berechnet:
![]() Gleichung 3
Gleichung 3
Die Übertragungsfunktion der z-Domäne ist:
 Gleichung 4
Gleichung 4
Der Frequenzgang ist:
![]() Gleichung 5
Gleichung 5
In Abbildung 5 entspricht SincN N identischen Sinc-Filtern in Serie. Der grafische Amplituden-/Frequenzgang des Sinusfilters hat ein kammartiges Aussehen (Abbildung 6).
 Abbildung 6: In den ADS1262/63 erzeugen die zahlreichen digitalen Sinc-Filter - wobei sinc2 zwei identischen SINC-Filtern in Serie und sinc3 drei identischen Sinc-Filtern in Serie entspricht usw. - bei 2400 Samples pro Sekunde (S/s) den kammartigen Frequenzgang. (Bildquelle: Texas Instruments)
Abbildung 6: In den ADS1262/63 erzeugen die zahlreichen digitalen Sinc-Filter - wobei sinc2 zwei identischen SINC-Filtern in Serie und sinc3 drei identischen Sinc-Filtern in Serie entspricht usw. - bei 2400 Samples pro Sekunde (S/s) den kammartigen Frequenzgang. (Bildquelle: Texas Instruments)
In Abbildung 6 sind die Spitzen und Nullstellen charakteristisch für die Sinusfilterreaktion. Die Frequenzgangnullstellen treten auf bei f(Hz) = N·FD, wobei N = 1, 2, 3, ... Bei den Nullfrequenzen hat der Filter null Verstärkung.
Sinc-Filter (in Reihe geschaltet) erzeugen eine erhöhte Dämpfung, was zu einer erhöhten Latenz führt. Wenn zum Beispiel eine bestimmte Sinusfilter-Berechnung mit einer externen Taktrate von 7,3728 MHz eine Ausgangsdatenrate von 14400 S/s ergibt, beträgt die Datenrate des Ausgangs des zweiten Sinusfilters 7200 S/s.
Der Tiefpass-FIR-Filter ist ein koeffizientenbasierter Filter. Der Filter hat eine gleichzeitige Dämpfung von 50 Hz und 60 Hz und Oberwellen bei Datenraten von 2,5 S/s bis 20 S/s. Die Konvertierungslatenzzeit der Datenraten des FIR-Filters entspricht einem einzigen Zyklus. Der FIR-Filter empfängt vorgefilterte Daten vom Sinc-Filter und dezimiert die Daten, um die Ausgangsdatenraten von 10 S/s zu erhalten (Abbildung 7).
 Abbildung 7: In den ADS1262/63 dämpft der FIR-Filter 50-Hz- und 60-Hz-Signale, um Störungen der Netzfrequenz zu reduzieren, und liefert eine Reihe von Antwortnullstellen, die in der Nähe dieser Frequenzen platziert sind. Die Nullen wiederholen sich bei den 50-Hz- und 60-Hz-Oberschwingungen. (Bildquelle: Texas Instruments)
Abbildung 7: In den ADS1262/63 dämpft der FIR-Filter 50-Hz- und 60-Hz-Signale, um Störungen der Netzfrequenz zu reduzieren, und liefert eine Reihe von Antwortnullstellen, die in der Nähe dieser Frequenzen platziert sind. Die Nullen wiederholen sich bei den 50-Hz- und 60-Hz-Oberschwingungen. (Bildquelle: Texas Instruments)
Der FIR-Filter dämpft 50-Hz- und 60-Hz-Signale, um Störungen der Netzfrequenz zu reduzieren, und bietet eine Reihe von Antwortnullstellen, die in der Nähe dieser Frequenzen platziert sind. Die Antwortnullstellen wiederholen sich bei den 50-Hz- und 60-Hz-Oberschwingungen.
Präziser rauscharmer ΔƩ-ADC
Ein hervorragendes Beispiel für einen rauscharmen ΔƩ-ADC ist der bereits erwähnte 24-Bit-Wandler ADS1235 von Texas Instruments mit Differenzeingängen.
Der ADS1235 ist ein präziser ΔƩ-ADC für 7200 S/s mit drei differentiellen oder fünf unsymmetrischen Eingängen und einem integrierten Verstärker mit programmierbarer Verstärkung (PGA) mit Verstärkungen von 1, 64 und 128. Dieses Bauteil enthält auch Diagnosefunktionen wie PGA-Überreichweiten- und Referenzmonitore. Der ADC liefert hochpräzise, driftfreie Konvertierungsdaten für hochpräzise Geräte, einschließlich Waagen, Dehnungsmessstreifen und resistive Drucksensoren (Abbildung 8).
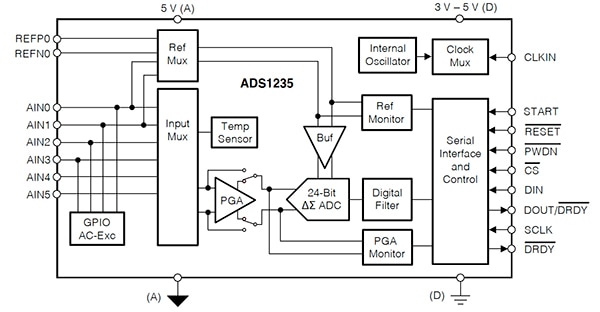 Abbildung 8: Blockschaltbild des 24-Bit-ΔƩ-ADCs ADS1235 mit sechskanaligem Analogeingang und GPIO-Eingangsmultiplexer. (Bildquelle: Texas Instruments)
Abbildung 8: Blockschaltbild des 24-Bit-ΔƩ-ADCs ADS1235 mit sechskanaligem Analogeingang und GPIO-Eingangsmultiplexer. (Bildquelle: Texas Instruments)
Für den ADS1235 sind die wesentlichen Faktoren, die die Rauschleistung beeinflussen, die Datenrate, die PGA-Verstärkung und der Chop-Modus. Langsamere Datenraten bringen die Eckfrequenz des digitalen Filters ein, wodurch das Rauschen reduziert wird. Darüber hinaus nimmt das Rauschen aufgrund einer Zwei-Punkt-Mittelung der Daten, die im Chop-Modus durchgeführt wird, im Vergleich zum Normalbetrieb um √2 ab.
Bei einer niedrigen Frequenz, einer Datenrate von 2,5 S/s und einer PGA-Verstärkung von 1 Volt/Volt beträgt das Wandlerrauschen am sinc3-Digitalausgang in einem 5-Volt-System 0,15 mVeff (0,3 mV Spitze-Spitze (PP)) mit einer effektiven Auflösung von 24 Bit sowie einer rauschfreien Auflösung von 24 Bit. Das theoretische wie auch das tatsächliche SNR dieses Geräts beträgt 146 dB. Tatsächlich erzeugen der stabile Modulator vierter Ordnung und die Filter sinc1 bis sinc4 unter diesen Bedingungen eine effektive Auflösung von 24 Bit sowie eine rauschfreie Auflösung von 24 Bit.
Der ADS1235 hat nahezu perfekte 24-Bit-Konvertierungen für eine Datenrate von 2,5 S/s realisiert. Die nächste Generation des ΔƩ-ADC in dieser Familie ist der ADS1262/63 von Texas Instruments. Der Hauptunterschied zwischen diesen Bausteinen besteht darin, dass der ADS1262/63 die rauscharme Schaltung verbessert und ein erweitertes 32-Bit-Ausgangsdatenregister bietet.
Der ADS1262/63 verfügt über einen verbesserten rauscharmen CMOS-PGA mit Verstärkungen von 1, 2, 4, 8, 16 und 32. Das flexible analoge Front-End (AFE) umfasst zwei Sensor-Erregerstromquellen, die für direkte RTD-Messungen geeignet sind (Abbildung 9).
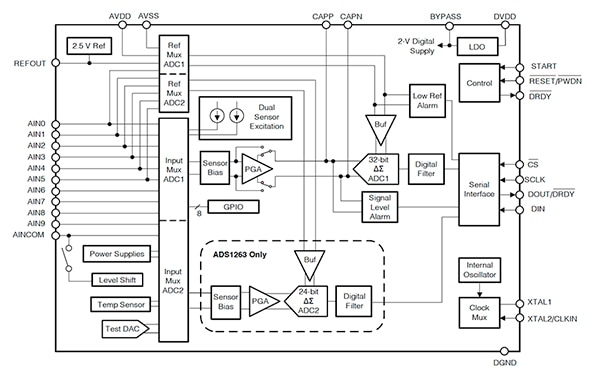 Abbildung 9: Das Blockschaltbild der 32-Bit-ΔƩ-ADCs ADS1262 und ADS1263 mit zehn-Kanal-Analogeingangsmultiplexer. Der ADS1263 bietet einen zweiten integrierten 24-Bit-ΔƩ-ADC. (Bildquelle: Texas Instruments)
Abbildung 9: Das Blockschaltbild der 32-Bit-ΔƩ-ADCs ADS1262 und ADS1263 mit zehn-Kanal-Analogeingangsmultiplexer. Der ADS1263 bietet einen zweiten integrierten 24-Bit-ΔƩ-ADC. (Bildquelle: Texas Instruments)
Wie beim ADS1235 sind auch bei den ADS1262/63 die PGA-Verstärkung, die Datenrate, der Digitalfilter-Modus und der Chop-Modus die wesentlichen Faktoren, die die Rauschleistung beeinflussen. Mit einer 32-Bit-Auflösung stellen die ADS1262/63 die Fähigkeit zur rauscharmen Tiefenstaffelung wirklich unter Beweis.
Ein stabiler Modulator vierter Ordnung und die Filter sinc1 bis sinc4 führen zunächst zu einer effektiven Auflösung von 32 Bit sowie zu einer rauschfreien Auflösung von 24 Bit. Durch die Konfiguration einer niedrigen Frequenz, einer Datenrate von 2,5 S/s und einer PGA-Verstärkung von 1 Volt/Volt (überbrückt) beträgt das Wandlerrauschen des digitalen sinc3-Ausgangs in einem 5-Volt-System 0,08 mVeff (0,307 mVPP). Dieses Gerät übertrifft die effektive Auflösung mit 26,9 Bit, sowie eine rauschfreie Auflösung von 25 Bit. Für dieses 32-Bit-System beträgt das theoretische SNR 387 dB, wobei das tatsächliche SNR 164 dB beträgt.
Die Unterschiede zwischen dem Rauschen der 24-Bit- und 32-Bit-Wandler sind deutlich, wobei die rauscharme Fähigkeit des 32-Bit-ΔƩ-ADCs die des 24-Bit-ΔƩ-ADCs übertrifft (Tabelle 2).
*Anmerkung: SNR = 6,02 N + 1,76, wobei N die Anzahl der Bits ist
|
Tabelle 2: Vergleich von ADC-Effektivwert-Rauschen, Spitze-Spitze-Rauschen und SNR mit der vollen Eingangsspannung von 5 Volt. (Datenquelle: DigiKey)
Fazit
Der ΔƩ-ADC reduziert das Rauschen mit immer neuen Fähigkeiten weiter gegen Null. Dieser Artikel zeigt, wie dieser nahezu digitale, rauscharme ADC direkt auf Temperatur-, Druck- und Wägezellenanwendungen abgebildet wird. Eine grundsätzliche Diskussion über einen präzisen 24-Bit-ΔƩ-ADC und einen 32-Bit-ΔƩ-ADC skizziert den Weg zur Realisierung ihrer ultrapräzisen Eigenschaften.

Haftungsausschluss: Die Meinungen, Überzeugungen und Standpunkte der verschiedenen Autoren und/oder Forumsteilnehmer dieser Website spiegeln nicht notwendigerweise die Meinungen, Überzeugungen und Standpunkte der DigiKey oder offiziellen Politik der DigiKey wider.






