Kann ein ADC ein Zufallszahlengenerator sein?

Wie gut ist ein ADC? Bei dieser Frage geht es nicht darum, wie viele Bits Auflösung er hat; es mag überraschen, dass ein 16-Bit-ADC nicht immer 16 Bits an nützlichen Informationen liefert! „Viele 16-Bit-ADCs arbeiten in Wirklichkeit als 7-Bit-ADCs und 9-Bit-Zufallszahlengeneratoren,“ sagt Mike Stone in „Choosing an ADC“. In diesem Artikel wird gezeigt, wie man feststellen kann, ob ein ADC mehr Zufallszahlen als nützliche Zahlen generiert, und es werden einige einfache Möglichkeiten zur Reduzierung der Zufallszahlen aufgezeigt.

Betrachten wir einen vereinfachten Aufbau: Ein ADC misst die Spannung an einem Fotowiderstand. Wenn der 12-Bit-ADC in Abbildung 1 (mit V_FS = 3,3 V) einen Wert von 2048 meldet, bedeutet das dann, dass die Spannung am Fotowiderstand 1,65 V beträgt?

Abbildung 1: Vereinfachter ADC-Aufbau zur Messung einer Fotowiderstandsspannung. (Bildquelle: Nathan Jones)

Nein, nicht wirklich! Zur Veranschaulichung nehmen Sie eine zweite Probe, dann eine dritte und schließlich 100.000 Abtastwerte und zeichnen Sie die Ergebnisse auf. Es wird eine Verteilung von ADC-Werten angezeigt (Abbildung 2); wenn sich an der Anordnung nichts geändert hat, könnte jeder dieser Werte die tatsächliche Spannung am Fotowiderstand sein, wobei der wahrscheinlichste Kandidat der Durchschnittswert all dieser Abtastungen ist.

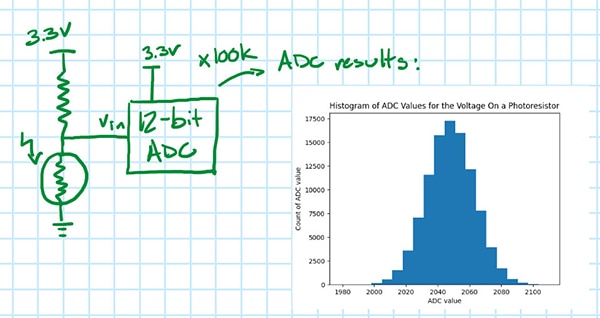Abbildung 2: Das eingefügte Bild zeigt das Histogramm der ADC-Werte für 100.000 Abtastwerte der Fotowiderstandsspannung. (Bildquelle: Nathan Jones)

Das wirft eine weitere Frage auf. Könnte ein Teil dieser Schwankungen auf tatsächliche Schwankungen des Eingangssignals zurückzuführen sein? Ja, das könnte es. Um dies zu testen, wird der Widerstandsteiler gegen eine Referenzspannung (Abbildung 3) mit bekanntem Rauschpegel ausgetauscht und der Versuch wiederholt.

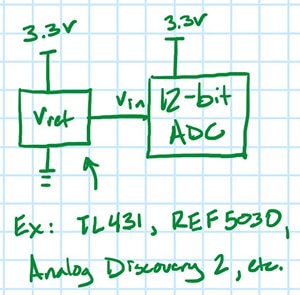Abbildung 3: Neuer Prüfaufbau mit einer Spannungsreferenz anstelle des Widerstandsteilers. (Bildquelle: Nathan Jones)

Idealerweise sollte die verwendete Spannungsreferenz einen Rauschpegel aufweisen, der weniger als 1/3 des im ADC erwarteten Rauschpegels beträgt (z. B. wenn der ADC ein Rauschen von ±1 LSB aufweisen soll [was bei Verwendung des ADC im obigen Beispiel ±0,8 mV wäre], dann sollte die Spannungsreferenz idealerweise einen Rauschpegel von weniger als 0,27 mV_ss aufweisen); wenn dies der Fall ist, dann wird erwartet, dass das gesamte gemessene Rauschen vom ADC stammen muss, basierend auf der Tatsache, dass sich unkorreliertes Rauschen im Quadrat addiert (Gleichung 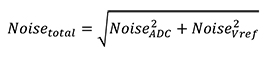1).

[1]

Wenn Noise_Vref = Noise_ADC/3 dann Noise_total = 1,054 × Noise_ADC. Dies würde bedeuten, dass die Spannungsreferenz nur 5,4% zum Gesamtrauschen beiträgt, ein vernachlässigbarer Betrag. Wenn sich herausstellt, dass das Rauschen der Spannungsreferenz größer ist als 1/3 des Rauschens des ADC, denken Sie daran, ihren Beitrag von der gemessenen Standardabweichung zu subtrahieren (siehe Gleichung 2).

[2]

Wie erkennt man den Rauschpegel einer Spannungsquelle?

Am einfachsten ist es, sie auf dem Datenblatt zu finden. Das folgende Beispiel aus dem Datenblatt des REF5030 von Texas Instruments zeigt, dass er einen Rauschpegel von 9 μV_ss hat.

Abbildung 4: Auszug aus dem REF5030-Datenblatt, das die Spezifikation des Ausgangsspannungsrauschens zeigt. (Bildquelle: Texas Instruments)

Wenn im Datenblatt kein Rauschpegel angegeben ist (oder um den Wert zu überprüfen), messen Sie ihn einfach mit einem Oszilloskop, wobei der Grundrauschpegel des Oszilloskops vorher bekannt sein muss. Dazu wird einer der Oszilloskopeingänge mit Masse verbunden und der Effektivwert der Signalschwankungen gemessen. Abbildung 5 zeigt das Ergebnis mit einem Analog Discovery 2 (AD2) und zeigt, dass der Effektivwert des Rauschens etwa 0,9 mV beträgt. Interessanterweise sinkt dieser Wert (bis in den µV-Bereich), wenn die Zeitbasis über 8 µs/div hinaus erhöht wird, vermutlich weil der AD2 Oversampling und Dezimierung verwendet, um seine effektive Auflösung zu erhöhen.

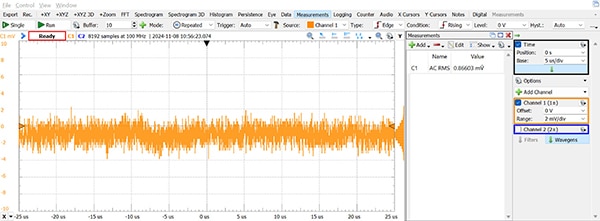Abbildung 5: Darstellung des Rauschpegels des Oszilloskops Analog Discovery 2. (Bildquelle: Nathan Jones)

Wenn die Spannungsquelle gemessen wird, sind alle Schwankungen im Oszilloskopsignal das Ergebnis des kombinierten Rauschens der Spannungsquelle und des Oszilloskops. Solange diese Rauschquellen unkorreliert sind (und das sind sie), ist Noise_measured = √(Noise²_Scope+Noise²_Vref) und Noise_Vref = √(Noise²_measured-Noise²_Scope), wie oben. Bei der Messung eines 2V_DC-Signals, das vom AD2 erzeugt wurde, wurde ein Rauschen von 1,2 mV festgestellt (Abbildung 6).

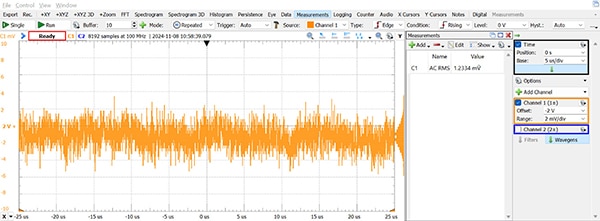Abbildung 6: Diese Darstellung eines 2VDC-Signals zeigt, dass das Rauschen des Oszilloskops 1,2 mV betrug. (Bildquelle: Nathan Jones)

Dies würde bedeuten, dass der Signalgenerator des AD2 ebenfalls einen Rauschpegel von etwa 0,9 mV aufweist. Dies ist niedrig genug, um einen 10-Bit-ADC zu testen (0,9 mV ist weniger als 1/3 eines LSB für einen 10-Bit-ADC mit 3,3 V Messbereichsendwert); bei ADCs mit höherer Auflösung müsste dieses Rauschen bei den Messungen berücksichtigt werden.

Abbildung 7: Das eingefügte Bild zeigt das neue Histogramm der ADC-Werte für 100.000 Abtastungen der Fotowiderstandsspannung mit der Spannungsreferenz. (Bildquelle: Nathan Jones)

Das ist viel besser! Beachten Sie nun, dass das zweite Histogramm (Abbildung 7) auf der x-Achse nur bis 2052 reicht (die Verteilung in diesem Diagramm [Abbildung 8] hat eine Standardabweichung von 1 LSB), während das erste Diagramm bis 2100 reichte (es hatte eine Standardabweichung von 15 LSBs). Dies wird als DC-Histogramm-Test für einen ADC bezeichnet, und die Standardabweichung zeigt effektiv an, wie viel Rauschen im ADC vorhanden ist: Jedes Mal, wenn ein Wert mit dem ADC gemessen wird, besteht nur eine Chance von 68%, dass der wahre Wert am Analogpin tatsächlich innerhalb von ±1 Standardabweichung dieses Wertes liegt, aber es besteht eine Chance von 99,7%, dass der wahre Wert innerhalb von ±3 Standardabweichungen dieses Wertes liegt.

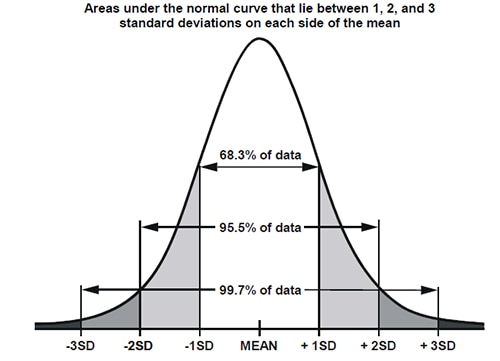Abbildung 8: Verteilungskurve mit Standardabweichungen. (Bildquelle: https://i.sstatic.net/jkMDV.png)

Die Umrechnung dieser Standardabweichung von LSBs in Volt ergibt das eingangsbezogene Rauschen für den ADC (Gleichung 3).

[3]

Wenn der ADC so rauscharm ist, dass alle ADC-Codes tatsächlich in ein einziges Bin fallen, versuchen Sie, die ADC-Referenzspannung zu verringern. Der Rauschpegel bleibt gleich, nimmt aber mehr ADC-Codes in Anspruch als zuvor, so dass ein geeigneter Wert für das eingangsbezogene Rauschen gefunden werden kann.

Die effektive Auflösung und die rauschfreie Codeauflösung (NFCR) eines ADC stellen das Ausmaß dar, in dem dieses Rauschen die ADC-Auflösung einschränkt. Sie werden berechnet, indem der gesamte Bereich der ADC-Codes in Bins unterteilt wird, die nur so breit sind wie entweder eine (Gleichung 4) oder 6,6 Standardabweichungen (Gleichung 5).

[4]

[5]

Im Wesentlichen gibt es weniger tatsächliche Bits im Ergebnis, da die Wahrscheinlichkeit, dass die letzten Bits im ADC-Ergebnis falsch oder verrauscht sind, zunimmt.

Eine etwas einfachere Version des DC-Histogramm-Tests besteht darin, einfach den Eingang des ADC zu erden und dann ein Histogramm (Abbildung 9) der ADC-Ergebnisse zu erstellen, wie es für das Oszilloskop gemacht wurde.

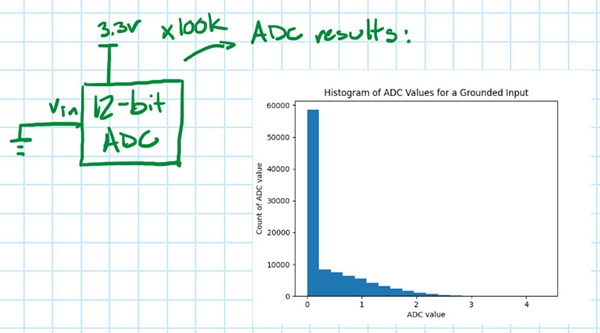Abbildung 9: Das eingefügte Bild zeigt das Histogramm der ADC-Abtastungen der Ausgangsspannung bei geerdetem Eingang. (Bildquelle: Nathan Jones)

Die Standardabweichung dieses Histogramms ist ebenfalls ein Maß für das ADC-Rauschen (abzüglich der Beiträge des Rauschens in der ADC-Referenzspannung, die sich nicht auf Messwerte von 0 V auswirkt), aber sie ist optimistischerweise niedrig. Der ADC meldet Werte unter 0 V wahrscheinlich einfach als 0, so dass nur die Hälfte der wahren Rauschverteilung zu sehen ist. In diesem Fall könnte das ADC-Rauschen angenähert werden, wenn man annimmt, dass die Verteilung symmetrisch um ihren Mittelwert ist, indem man genügend Medianwerte in negative Zahlen ändert, so dass die Verteilung symmetrisch wird, und dann die Standardabweichung davon berechnet (Abbildung 10).

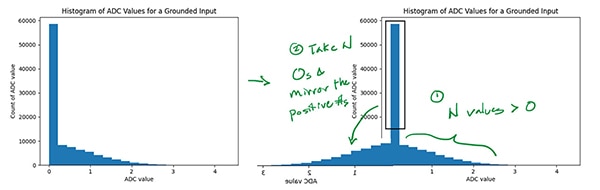Abbildung 10: Spiegelung des Histogramms aus Abbildung 9 zur Annäherung an das ADC-Rauschen. (Bildquelle: Nathan Jones)

Was kann man also gegen all dieses Rauschen tun? Wenn die Auflösung des ADC noch innerhalb der Projektanforderungen liegt (Glück gehabt!), dann sollten Sie bedenken, dass jede ADC-Messung mit einer gewissen Unsicherheit verbunden ist:

• Wenn Sie zwei ADC-Werte vergleichen, betrachten Sie sie nur dann als gleichwertig, wenn sie innerhalb von 6,6 σ voneinander liegen (um 99,7% sicher zu sein) oder wenn sie innerhalb von σ voneinander liegen (um nur 68% sicher zu sein).
• Wenn Sie einen ADC-Wert mit einem Schwellenwert vergleichen, fügen Sie dem Schwellenwertvergleich eine gewisse Hysterese hinzu (wie bei einem Thermostat), um zu vermeiden, dass das eingebettete System aufgrund von Rauschen den Schwellenwert über- oder unterschreitet.

Wenn sich herausstellt, dass der ADC die Projektanforderungen nicht mehr erfüllt, gibt es ein paar einfache Möglichkeiten, seine Performance zu verbessern. Auf der Hardwareseite sind dies unter anderem:

• Verwendung einer rauschärmeren Referenz (wie z. B. dem REF5030 von Texas Instruments oder dem TL431 von EVVO) für AVCC und AREF
• Sicherstellung eines minimalen Übersprechens zwischen analogen und digitalen Signalen auf der Leiterplatte
• Abschalten der CPU während ADC-Wandlungen (falls die MCU dies unterstützt), um digitales Rauschen zu reduzieren

Softwareseitig kann das Eingangssignal überabgetastet werden (d. h. es wird der Durchschnitt von N Abtastwerten genommen), um das Rauschen zu reduzieren, obwohl dies die maximale Abtastrate deutlich verringert. (In der Tat könnte eine Technik namens „Überabtastung und Dezimierung“ verwendet werden, um die Auflösung des ADC um einen Betrag zu erhöhen, der mit der Anzahl der Überabtastung des Eingangs zusammenhängt!)

Angenommen, die Standardabweichung eines DC-Histogramm-Tests für die Ersteinrichtung beträgt 1 LSB. Wenn der ADC 2048 anzeigt, bedeutet das nun (mit einer Wahrscheinlichkeit von 68% ), dass der wahre Wert 1,650±0,008 V (Abbildung 11) beträgt?

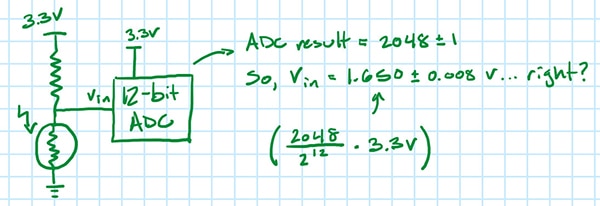Abbildung 11: Angenommen, die Standardabweichung des in Abbildung 1 dargestellten Aufbaus beträgt 1 LSB und der ADC-Ausgang ist 2048, beträgt die wahre Eingangsspannung 1,650±0,008 V? (Bildquelle: Nathan Jones)

Näher dran, aber immer noch nicht! Das liegt daran, dass alle ADCs Probleme mit der Messung eines sich schnell ändernden Eingangssignals bei einer bestimmten Frequenz haben, was zu ungenauen Messungen (d. h. Rauschen) führt. Überraschenderweise kann die Frequenz, bei der dies geschieht, weit unter der maximalen Abtastrate des ADC liegen! Das bedeutet, dass ein 12-Bit-ADC mit einer Abtastrate von 1 MS/s (Mega-Samples pro Sekunde) bei Eingangssignalen nahe 500 kHz möglicherweise keine 12-Bit-Auflösung hat; die Auflösung des ADC kann auf 6 Bit oder weniger fallen, wenn die Eingangssignalfrequenz so hoch ist. Wenn Sie versuchen, ein Signal am Fotowiderstand zu messen, das über 10 Hz liegt, kann es sein, dass der ADC keine 12-Bit-Auflösung hat.

Um festzustellen, wie gut die Auflösung des ADC bei höheren Eingangsfrequenzen ist, senden Sie ein bekanntes Signal (in diesem Fall eine Sinuswelle) und messen Sie, wie gut die ADC-Werte mit diesem bekannten Signal übereinstimmen (Abbildung 12). (Ist die Sinuskurve „gut genug“? Dies wird nach der Bekanntgabe des Verfahrens zur Durchführung des Tests erörtert werden; dann wird es mehr Sinn machen).

Abbildung 12: Testaufbau mit einem bekannten Sinuswellen-Eingang. (Bildquelle: Nathan Jones)

Für die Sinuswelle kann ein Funktionsgenerator (wie er in vielen USB-Oszilloskopen zu finden ist), ein DDS-Chip (wie der AD9834 von Analog Devices) oder ein eigener Sinuswellengenerator verwendet werden (z. B. auf der Grundlage eines Wien-Brückenoszillators oder unter Verwendung eines MAX7400 von Analog Devices zur Tiefpassfilterung einer Rechteckwelle). Es ist wichtig zu beachten, dass für diesen Test nur Eingangsfrequenzen verwendet werden sollten, die keine ganzzahligen Vielfachen der Abtastfrequenz sind (z. B. sollte keine Eingangsfrequenz von 1 kHz verwendet werden, wenn die Abtastrate 100 kHz beträgt). Damit soll vermieden werden, dass die Sinuswelle bei jedem Zyklus fälschlicherweise an denselben Stellen abgetastet wird. Um den ADC maximal zu belasten, stellen Sie die Amplitude der Eingangssinuswelle auf den größten Wert ein, der den Ausgang nicht „beschneidet“ (z. B. etwas weniger als 1,65 V für den ADC in den obigen Beispielen).

Nach der Erfassung der ADC-Ergebnisse werden die Daten an eine Sinuswelle angepasst, um den Restfehler zu berechnen. Die Sinuswellenanpassung kann mit fast jeder Datenmenge durchgeführt werden, aber um die besten Ergebnisse zu erzielen, müssen mindestens fünf volle Perioden der Eingangssinuswelle vorhanden sein. Es ist wahrscheinlich, dass der Sinus-Anpassungsalgorithmus initialisiert werden muss, indem man ihm Anfangsschätzungen für Amplitude, Frequenz, Phasenverschiebung und Offset gibt (Abbildung 13).

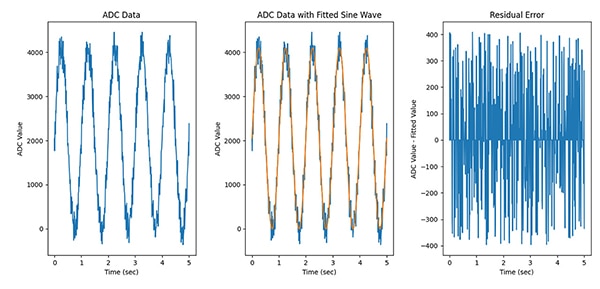Abbildung 13: Mithilfe eines Algorithmus zur Sinuswellenanpassung kann der Restfehler bestimmt werden. (Bildquelle: Nathan Jones)

Dieser Test wird als Sinuswellen-Anpassungstest für einen ADC bezeichnet, und der Effektivwert des Restfehlers ist ein Maß dafür, wie verrauscht der ADC bei dieser spezifischen Eingangsfrequenz ist. Bei niedrigen Frequenzen sollte das effektive Rauschen mit dem eingangsbezogenen Rauschen aus dem DC-Histogrammtest übereinstimmen, aber bei höheren Frequenzen wird es mit ziemlicher Sicherheit durch die oben erwähnten frequenzabhängigen Rauschquellen beeinträchtigt.

Der effektive Rauschwert aus dem Sinuswellen-Anpassungstest kann zur Berechnung der effektiven Anzahl von Bits (ENOB) des ADC verwendet werden (Gleichung 6), d. h. der Anzahl von Bits eines idealen ADC, dessen einzige Rauschquelle, das Quantisierungsrauschen, denselben Effektivwert hat wie das Rauschen im ADC.

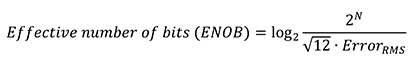[6]

Dieser Wert ist spezifisch für die Frequenz des verwendeten Eingangssignals. Um ein vollständigeres Bild des ADC zu erhalten, sollte dieser Test bei Frequenzen bis zum höchsten Eingangssignal von Interesse oder bis zur Hälfte der maximalen Abtastrate wiederholt werden. Es kann sein, dass das Rauschen bei Frequenzen weit unter der Hälfte der maximalen Abtastrate stark ansteigt (und die ENOB stark abfällt!). Zum Beispiel wurde genau diese Testreihe mit dem ADC in einem STM32F042K6 von STMicroelectronics durchgeführt und die Ergebnisse aufgezeichnet (Abbildung 14).

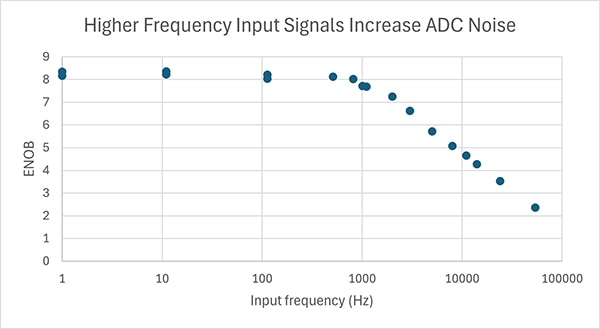Abbildung 14: Frequenzrauschtest für einen ADC in einem Mikrocontroller STM32F042K6. (Bildquelle: Nathan Jones)

Obwohl der ADC auf dem Mikrocontroller STM32F042K6 mit 1 MHz abtasten kann, fällt die Auflösung oberhalb von 1 kHz ab. Wollte man mit diesem ADC ein 10-kHz-Signal messen, so hätte man an diesem Punkt nur noch eine Auflösung von etwa 5 Bit! (Beachten Sie auch, dass die maximale ENOB bei etwa 8,3 liegt; dies ist auf ~10 LSBs Rauschen selbst bei Gleichstrom zurückzuführen, die die effektive Auflösung des ADC von 12 Bits auf etwa 8,7 Bits reduzieren, und zwar von Anfang an. Diese Tests wurden auf einer nicht modifizierten Nucleo-F042-Entwicklungsplatine von STMicroelectronics durchgeführt; die Ergebnisse wären wesentlich besser, wenn eine der oben genannten Techniken verwendet würde [„Okay, was kann man also gegen dieses Rauschen tun?“]).

Wie erkennt man den Rauschpegel einer Sinuswelle?

Wie bei der Spannungsreferenz muss der Rauschpegel der Sinuswelle mit einem Oszilloskop gemessen werden, wenn er a priori angenommen wird (d. h. wenn er nicht in einem Datenblatt angegeben ist). Mit der bereits erwähnten Technik der Sinuswellenanpassung kann das Rauschen des Sinuswellengenerators charakterisiert werden.

1. Bestimmen Sie zunächst das Grundrauschen des Oszilloskops, indem Sie den Eingang mit Masse verbinden und den Effektivwert des Ausgangs berechnen (wie bereits im Abschnitt „Wie erkennt man den Rauschpegel einer Spannungsquelle“ beschrieben).
2. Messen Sie dann das Ausgangssignal des Sinusgenerators, passen Sie die Ergebnisse an eine perfekte Sinuswelle an und berechnen Sie den Effektivwert der Residuen. Verwenden Sie dann Gleichung 2, um das Rauschen des Sinusgenerators zu bestimmen (unter Verwendung des Grundrauschens des Oszilloskops als Näherung für sein Wechselstromrauschen).

Im Idealfall beträgt der Rauschpegel der Sinuswelle weniger als 1/3 des vom ADC erwarteten Rauschpegels (mit anderen Worten, die Sinuswelle ist „spektral rein“), so dass ihr Beitrag zum gemessenen Rauschen vernachlässigbar wäre. Wenn der Rauschpegel der Sinuswelle höher ist als dieser Wert, muss er vom gemessenen Rauschen abgezogen werden, das durch die Berechnung der Effektivwerte des Restfehlers erhalten wird.

Dieser Test sollte für jede Eingangsfrequenz wiederholt werden, die zum Testen des ADC verwendet werden soll (selbst der Sinusgenerator kann frequenzabhängige Rauschquellen haben!).

Was kann man gegen dieses Rauschen tun? Zunächst wird empfohlen, einen Tiefpassfilter (LPF) zwischen die Signalquelle und den ADC zu schalten, dessen Grenzfrequenz knapp über dem höchsten interessierenden Signal liegt, um hochfrequentes Rauschen zu begrenzen (dies ist generell eine „gute Maßnahme“ für jedes Datenerfassungssystem). Wenn das interessierende Signal mit der höchsten Frequenz unterhalb des „Knies“ im Diagramm von ENOB und Eingangsfrequenz liegt, gibt es keinen Auflösungsverlust. Wenn man versucht, Signale oberhalb dieses „Knies“ zu messen, gibt es ein paar Möglichkeiten, die Auflösung bei höheren Frequenzen zu verbessern. Dazu gehören:

• Sicherstellen, dass die Ausgangsimpedanz des Geräts, das mit dem analogen Anschluss verbunden ist, sehr niedrig ist, eventuell Einfügen eines Operationsverstärkers zur Pufferung
• Einstellen des ADC-Takts oder der Abtast-/Haltezeit auf die höchstmögliche Geschwindigkeit, wobei der interne Kondensator noch genügend Zeit zum Aufladen haben sollte
• Verwendung einer ADC-Taktquelle mit geringem Jitter und Konfiguration des Systems, um ADC-Abtastungen in regelmäßigen Abständen vorzunehmen

Sofern nicht ein Signal in einem sehr schmalen Frequenzband angestrebt wird, ist es am einfachsten, davon auszugehen, dass die tatsächlichen Eingangssignale von DC bis zur Grenzfrequenz des Tiefpassfilters den gleichen Frequenzgehalt haben und dass daher das effektive Rauschen in jeder ADC-Messung das durchschnittliche effektive Rauschen ist, das mit dem Sinuswellenanpassungstest von DC bis zur Grenzfrequenz gemessen wurde. Wenn mit dem bereits erwähnten STM32F042K6 breitbandige Signale bis zu 10 kHz gemessen werden sollen, wäre es am besten, so zu arbeiten, als ob der ADC nur eine ENOB von etwa 6 Bit für jede Messung hätte. Dieser Wert kann sehr wohl niedriger sein als der mit dem DC-Histogramm-Test ermittelte, was darauf hindeutet, dass die Sicherheit der einzelnen ADC-Messungen geringer ist, wenn die Möglichkeit besteht, dass sie einen höheren Frequenzgehalt aufweisen.

Die nächste zu berücksichtigende Maßnahme ist das Hinzufügen eines Tiefpassfilters zwischen dem Sensor und dem ADC, so dass das effektive Rauschen von DC bis zur Grenzfrequenz nur ±1 LSB beträgt. Wenn der ADC 2048 anzeigt, bedeutet das jetzt endlich (mit einer Wahrscheinlichkeit von 68% ), dass der wahre Wert 1,650 ±0,008 V beträgt (Abbildung 15)?

Abbildung 15: Führt das Hinzufügen eines Tiefpassfilters in der Schaltung zu einem wahren Wert von 1,650±0,008 V? (Bildquelle: Nathan Jones)

So verrückt es auch klingt, aber leider immer noch nicht! In diesem Artikel wurde zwar das Rauschen des ADC beschrieben, aber noch nicht sein Fehler. Nach den hier beschriebenen Tests besteht die einzige Sicherheit darin, dass zwei ADC-Werte gleich oder unterschiedlich sind. Es ist jedoch nicht bekannt, ob ein ADC-Code von 2048 exakt 1,65 V oder einem anderen Wert entspricht. Verstärkungs-, Offset- und differentielle Nichtlinearitätsfehler (neben anderen) können bedeuten, dass die Umwandlung eines ADC-Codes in eine tatsächliche Spannung komplizierter ist als die Verwendung von V_in = ADC-Ergebnis × V_FS/2^N. Aber das ist ein Thema für einen anderen Artikel!

Referenzen

1. Charakterisierung des ADCs des Raspberry Pi Pico
2. Grundlagen zu Datenwandlern (Texas Instruments)
3. Grundlagen zu SINAD, ENOB, SNR, THD, THD + N und SFDR, damit Sie sich nicht im Grundrauschen verlieren (Analog Devices)
4. Die guten, die schlechten und die hässlichen Aspekte des ADC-Eingangsrauschens - ist kein Rauschen ein gutes Rauschen? (Analog Devices)
5. Das Beste aus dem ADC des SAM D21 herausholen (Thea Codes)
6. Prüfung von Analog/Digital-Wandlern (Kent Lundberg)
7. Dynamische Tests für die Performance von A/D-Wandlern (Texas Instruments)
8. Optimierung der ADC-Genauigkeit in den STM32-MCUs (STM)
9. Verbesserung der ADC-Auflösung durch Überabtastung (Atmel)
10. Grundlagen der ADC-Präzisionsrauschanalyse (Texas Instruments)
11. ADC-Verstärkung und Offset-Fehlerkalibrierung auf ARM®-Cortex®-M0+-basierten MCUs (Microchip)
12. Erzeugung einer Sinuswelle durch Tiefpassfilterung einer Rechteckwelle
13. Auswirkungen des Rauschens von Digitalisierern auf Oszilloskopmessungen (EE Times)
14. Verständnis der effektiven Anzahl von Bits (robuster Schaltungsentwurf)